ALE 1D

Substitution for Integrals

• Substitution for Definite Integrals

• Substitution for Definite Integrals-math.libretexts.org

• Lesson Explainer: Integration by Substitution: Definite Integrals

• Substitution Rule for Indefinite Integrals

In the ALE description of motion, neither the material configuration \(R_{\boldsymbol\xi}\) nor the spatial configuration \(R_{\mathbf{x}}\) is taken as the reference. Thus, a third domain is needed: the referential configuration \(R_{\boldsymbol\eta}\) where reference coordinates \({\boldsymbol\eta}\) are introduced to identify the grid points. The following figure shows these domains and the one-to-one transformations relating the configurations. The referential domain \(R_{\boldsymbol\eta}\) is mapped into the material and spatial domains by \({\boldsymbol\Psi}\) and \({\boldsymbol\Phi}\) respectively. The particle motion \({\boldsymbol{\varphi}}\) may then be expressed as \({\boldsymbol{\varphi}}={\boldsymbol\Phi}\circ{\boldsymbol\Psi}^{-1}\), clearly showing that, of course, the three mappings \({\boldsymbol\Psi}\), \({\boldsymbol\Phi}\), and \({\boldsymbol{\varphi}}\) are not independent.

The motion of the ALE computational mesh is independent of the material motion.

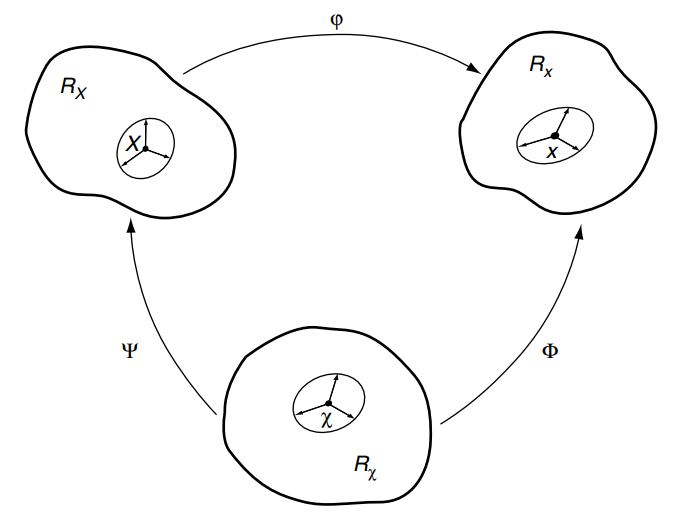
Some Example

Example 1:

\[\begin{split}\begin{align} x & = \varphi(\xi,t) = \xi +t \\ x & = \phi(\eta,t) = \eta +2t \\ x & =\varphi(\xi,t)=\phi(\eta,t) \Rightarrow \xi +t =\eta +2t \Rightarrow \xi =\eta +t\\ \xi &=\psi(\eta,t)=\eta +t\\ \eta &=\psi^{-1}(\xi,t)=\xi-t\\ \end{align}\end{split}\]

the fluid particle velocity is

\[v_{\text{fluid}}=\cfrac{\text{d} x}{\text{d} t}\Bigg|_{\xi}=\cfrac{\partial \varphi(\xi,t)}{\partial t}=1\]

the mesh particle velocity is

\[\begin{split}v_{\text{mesh}}=\cfrac{\text{d} x}{\text{d} t}\Bigg|_{\eta}=\cfrac{\partial \phi(\eta ,t)}{\partial t}=2\\\end{split}\]

Let

\[\begin{split}\begin{align} f(x,t)&=x-t\\ f(x,t)&=x-t=f(\varphi(\xi,t),t)=(\xi +t)-t=\xi =f^{*}(\xi,t)\\ f(x,t)&=f^{*}(\xi,t)=f^{*}(\psi(\eta,t),t)=f^{**}(\eta,t)=\xi=\eta +t\\ \end{align}\end{split}\]

then there is

\[\begin{split}\begin{align} f^{*}(\xi,t)&=\xi\\ \cfrac{\text{d}\bar{f} }{\text{d} t}&\equiv \cfrac{\partial f^{*}(\xi,t)}{\partial t}=0\\ \end{align}\end{split}\]

\[\begin{split}\begin{align} \cfrac{\text{d}f(x,t)}{\text{d} t}\Bigg|_{\xi}\equiv \cfrac{\partial f^{*}(\xi,t)}{\partial t} &=\cfrac{\partial f(x,t)}{\partial t}+\cfrac{\partial f(x,t)}{\partial x}\cfrac{\partial x(\xi,t)}{\partial t}\\ &=\cfrac{\partial f(x,t)}{\partial t}+\cfrac{\partial f(x,t)}{\partial x}\cfrac{\partial \varphi(\xi,t)}{\partial t}\\ &=\cfrac{\partial (x-t)}{\partial t}+\cfrac{\partial (x-t)}{\partial x}\cfrac{\partial (\xi +t) }{\partial t}\\ &=-1+1=0\\ \end{align}\end{split}\]

\[\begin{split}\begin{align} \cfrac{\text{d}f^{**}(\eta,t)}{\text{d} t}\Bigg|_{\xi}\equiv \cfrac{\partial f^{*}(\xi,t)}{\partial t} &=\cfrac{\partial f^{**}(\eta,t)}{\partial t}+\cfrac{\partial f^{**}(\eta,t)}{\partial \eta}\cfrac{\partial \eta(\xi,t)}{\partial t}\\ &=\cfrac{\partial f^{**}(\eta,t)}{\partial t}+\cfrac{\partial f^{**}(\eta,t)}{\partial \eta}\cfrac{\partial \psi^{-1}(\xi,t)}{\partial t}\\ &=\cfrac{\partial (\eta +t)}{\partial t}+\cfrac{\partial (\eta +t)}{\partial \eta}\cfrac{\partial (\xi-t) }{\partial t}\\ &=1-1=0\\ \end{align}\end{split}\]

Example 2:

Let

\[\begin{split}\begin{align} f(x,t)&=x\\ f(x,t)&=x=f(\varphi(\xi,t),t)=\xi +t =f^{*}(\xi,t)\\ f(x,t)&=f^{*}(\xi,t)=f^{*}(\psi(\eta,t),t)=f^{**}(\eta,t)=\xi +t=\eta +2t\\ \end{align}\end{split}\]

then there is

\[\begin{split}\begin{align} f^{*}(\xi,t)&=\xi +t\\ \cfrac{\text{d}\bar{f} }{\text{d} t}&\equiv \cfrac{\partial f^{*}(\xi,t)}{\partial t}=1\\ \end{align}\end{split}\]

\[\begin{split}\begin{align} \cfrac{\text{d}f(x,t)}{\text{d} t}\Bigg|_{\xi}\equiv \cfrac{\partial f^{*}(\xi,t)}{\partial t} &=\cfrac{\partial f(x,t)}{\partial t}+\cfrac{\partial f(x,t)}{\partial x}\cfrac{\partial x(\xi,t)}{\partial t}\\ &=\cfrac{\partial f(x,t)}{\partial t}+\cfrac{\partial f(x,t)}{\partial x}\cfrac{\partial \varphi(\xi,t)}{\partial t}\\ &=\cfrac{\partial (x)}{\partial t}+\cfrac{\partial (x)}{\partial x}\cfrac{\partial (\xi +t) }{\partial t}\\ &=0+1=1\\ \end{align}\end{split}\]

\[\begin{split}\begin{align} \cfrac{\text{d}f^{**}(\eta,t)}{\text{d} t}\Bigg|_{\xi}\equiv \cfrac{\partial f^{*}(\xi,t)}{\partial t} &=\cfrac{\partial f^{**}(\eta,t)}{\partial t}+\cfrac{\partial f^{**}(\eta,t)}{\partial \eta}\cfrac{\partial \eta(\xi,t)}{\partial t}\\ &=\cfrac{\partial f^{**}(\eta,t)}{\partial t}+\cfrac{\partial f^{**}(\eta,t)}{\partial \eta}\cfrac{\partial \psi^{-1}(\xi,t)}{\partial t}\\ &=\cfrac{\partial (\eta +2t)}{\partial t}+\cfrac{\partial (\eta +2t)}{\partial \eta}\cfrac{\partial (\xi-t) }{\partial t}\\ &=2-1=1\\ \end{align}\end{split}\]