Inviscid Burgers Equation

1. CFD Julia: A Learning Module Structuring an Introductory Course on Computational Fluid Dynamics

Inviscid Burgers Equation: Non-Conservative Form

In this section, we discuss the solution of the inviscid Burgers equation which is a nonlinear hyperbolic partial differential equation. The hyperbolic equations admit discontinuities, and the numerical schemes used for solving hyperbolic PDEs need to be higher-order accurate for smooth solutions, and non-oscillatory for discontinuous solutions. The inviscid Burgers equation is given below

\[\cfrac{\partial u}{\partial t}+u\cfrac{\partial u}{\partial x}=0\]

Inviscid Burgers Equation: Conservative Form

In this section, we explain two approaches for solving the inviscid Burgers equation in its conservative form. The inviscid Burgers equation can be represented in the conservative form as below

\[\cfrac{\partial u}{\partial t}+\cfrac{\partial f}{\partial x}=0\]

where

\[f=\cfrac{u^{2}}{2}\]

The \(f\) is termed as the flux. We need to modify the grid arrangement to solve the inviscid Burgers equation in its conservative form.

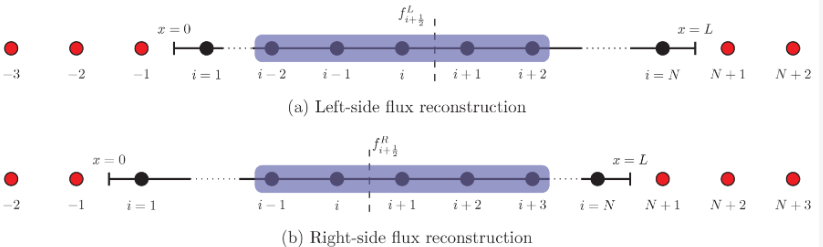
Finite difference grid for one-dimensional problems where the the solution is stored at the center of the cells. The flux is also computed at left and right boundary. The stencil required for reconstruction of left and right side flux is highlighted with blue rectangle. Ghost points are shown by red color.

The solution field is stored at the center of each cell and this type of grid is primarily used for finite volume discretization. We explain two approaches to compute the nonlinear term in the inviscid Burgers equation.

\[\Delta x=x_{i+1/2}-x_{i-1/2}\]

Flux Splitting

The conservative form of the inviscid Burgers equation allows us to use the flux splitting method and WENO reconstruction to compute the flux at the interface. In this method, we first compute the flux \(f\) at the nodal points. The nonlinear advection term of the inviscid Burgers equation is computed as

\[\cfrac{\partial f}{\partial x}\Bigg|_{x=x_{i}}=\cfrac{f_{i+1/2}-f_{i-1/2}}{\Delta x}\]

\[\cfrac{\partial f}{\partial x}\Bigg|_{x=x_{i}}=\cfrac{f^{L}_{i+1/2}-f^{L}_{i-1/2}}{\Delta x}+\cfrac{f^{R}_{i+1/2}-f^{R}_{i-1/2}}{\Delta x}\]

at a particular node \(i\), The superscripts \(L\) and \(R\) refer to the positive and negative flux component at the interface and the subscripts \(i-1/2\) and \(i+1/2\) for the left and right side interface of the nodal point \(i\). We use WENO-5 reconstruction to compute the left and right side flux at the interface. First, we compute the flux at nodal points and then split it into positive and negative components. This process is called as Lax-Friedrichs flux splitting and the positive and negative component of the flux at a nodal location is calculated as

\[\begin{split}\begin{array}{l} f^{+}_{i}=\cfrac{1}{2}(f_{i}+au_{i})\\ f^{-}_{i}=\cfrac{1}{2}(f_{i}-au_{i})\\ \end{array}\end{split}\]

where \(a\) is the absolute value of the flux Jacobian(\(a=\left | \cfrac{\partial f}{\partial u} \right |\)) We chose the values of \(a\) as the maximum value of \(u_{i}\) over the stencil used for WENO-5 reconstruction, i.e.,

\[a=max(|u_{i-2}|,|u_{i-1}|,|u_{i}|,|u_{i+1}|,|u_{i+2}|)\]

Once we split the nodal flux into its positive and negative component we reconstruct the left and right side fluxes at the interface using WENO-5 scheme using below formulas

\[\begin{split}\begin{align} f^{L}_{i+1/2} & = w^{L}_{0}(\cfrac{1}{3}f^{+}_{i-2}-\cfrac{7}{6}f^{+}_{i-1}+\cfrac{11}{6}f^{+}_{i})\\ &+w^{L}_{1}(-\cfrac{1}{6}f^{+}_{i-1}+\cfrac{5}{6}f^{+}_{i}+\cfrac{1}{3}f^{+}_{i+1})\\ &+w^{L}_{2}(\cfrac{1}{3}f^{+}_{i}+\cfrac{5}{6}f^{+}_{i+1}-\cfrac{1}{6}f^{+}_{i+2})\\ f^{R}_{i-1/2}& = w^{R}_{0}(-\cfrac{1}{6}f^{-}_{i-2}+\cfrac{5}{6}f^{-}_{i-1}+\cfrac{1}{3}f^{-}_{i})\\ & + w^{R}_{1}(\cfrac{1}{3}f^{-}_{i-1}+\cfrac{5}{6}f^{-}_{i}-\cfrac{1}{6}f^{-}_{i+1})\\ & + w^{R}_{2}(\cfrac{11}{6}f^{-}_{i}-\cfrac{7}{6}f^{-}_{i+1}+\cfrac{1}{3}f^{-}_{i+2}) \end{align}\end{split}\]

We use the third-order Runge-Kutta numerical scheme for time integration and periodic boundary condition for the domain. For the conservative form, we need three ghost points on left and right sides, since we compute the flux at the left and right boundary of the domain also. The periodic boundary condition for fluxes at ghost points is given by

\[\begin{split}\begin{array}{l} f_{-1}=f_{N-1}\\ f_{-2}=f_{N-2}\\ f_{-3}=f_{N-3}\\ \end{array}\end{split}\]

\[\begin{split}\begin{array}{l} f_{N}=f_{0}\\ f_{N+1}=f_{1}\\ f_{N+2}=f_{2}\\ \end{array}\end{split}\]

flux jacobian:

\[a_{i}=\left | \cfrac{\partial f}{\partial u} \right |=max(|u_{i-2}|,|u_{i-1}|,|u_{i}|,|u_{i+1}|,|u_{i+2}|)\]

\[\begin{split}\begin{array}{l} a_{0}=max(|u_{0-2}|,|u_{0-1}|,|u_{0}|,|u_{0+1}|,|u_{0+2}|) \\ a_{1}=max(|u_{1-2}|,|u_{1-1}|,|u_{1}|,|u_{1+1}|,|u_{1+2}|) \\ a_{2}=max(|u_{2-2}|,|u_{2-1}|,|u_{2}|,|u_{2+1}|,|u_{2+2}|) \\ \cdots\\ a_{i}=max(|u_{i-2}|,|u_{i-1}|,|u_{i}|,|u_{i+1}|,|u_{i+2}|) \\ \cdots\\ a_{N-3}=max(|u_{N-3-2}|,|u_{N-3-1}|,|u_{N-3}|,|u_{N-3+1}|,|u_{N-3+2}|) \\ a_{N-2}=max(|u_{N-2-2}|,|u_{N-2-1}|,|u_{N-2}|,|u_{N-2+1}|,|u_{N-2+2}|) \\ a_{N-1}=max(|u_{N-1-2}|,|u_{N-1-1}|,|u_{N-1}|,|u_{N-1+1}|,|u_{N-1+2}|) \\ \end{array}\end{split}\]

\[\begin{split}\begin{array}{l} a_{0}=max(|u_{-2}|,|u_{-1}|,|u_{0}|,|u_{1}|,|u_{2}|) \\ a_{1}=max(|u_{-1}|,|u_{0}|,|u_{1}|,|u_{2}|,|u_{3}|) \\ a_{2}=max(|u_{0}|,|u_{1}|,|u_{2}|,|u_{3}|,|u_{4}|) \\ \cdots\\ a_{i}=max(|u_{i-2}|,|u_{i-1}|,|u_{i}|,|u_{i+1}|,|u_{i+2}|) \\ \cdots\\ a_{N-3}=max(|u_{N-5}|,|u_{N-4}|,|u_{N-3}|,|u_{N-2}|,|u_{N-1}|) \\ a_{N-2}=max(|u_{N-4}|,|u_{N-3}|,|u_{N-2}|,|u_{N-1}|,|u_{N}|) \\ a_{N-1}=max(|u_{N-3}|,|u_{N-2}|,|u_{N-1}|,|u_{N}|,|u_{N+1}|) \\ \end{array}\end{split}\]

\[\begin{split}\begin{array}{l} a_{0}=max(|u_{N-2}|,|u_{N-1}|,|u_{0}|,|u_{1}|,|u_{2}|) \\ a_{1}=max(|u_{N-1}|,|u_{0}|,|u_{1}|,|u_{2}|,|u_{3}|) \\ a_{2}=max(|u_{0}|,|u_{1}|,|u_{2}|,|u_{3}|,|u_{4}|) \\ \cdots\\ a_{i}=max(|u_{i-2}|,|u_{i-1}|,|u_{i}|,|u_{i+1}|,|u_{i+2}|) \\ \cdots\\ a_{N-3}=max(|u_{N-5}|,|u_{N-4}|,|u_{N-3}|,|u_{N-2}|,|u_{N-1}|) \\ a_{N-2}=max(|u_{N-4}|,|u_{N-3}|,|u_{N-2}|,|u_{N-1}|,|u_{0}|) \\ a_{N-1}=max(|u_{N-3}|,|u_{N-2}|,|u_{N-1}|,|u_{0}|,|u_{1}|) \\ \end{array}\end{split}\]

flux at left interface:

\[\begin{split}\begin{array}{l} f^{L}_{i+1/2}=stencil(i-2,i-1,i,i+1,i+2)\\ f^{R}_{i-1/2}=stencil(i-2,i-1,i,i+1,i+2)\\ f^{R}_{i+1/2}=stencil(i-1,i,i+1,i+2,i+3)\\ \end{array}\end{split}\]

\[\begin{split}\begin{array}{l} f^{L}_{-1+1/2}=stencil(-1-2,-1-1,-1,-1+1,-1+2)\\ f^{L}_{0+1/2}=stencil(0-2,0-1,0,0+1,0+2)\\ f^{L}_{1+1/2}=stencil(1-2,1-1,1,1+1,1+2)\\ \cdots\\ f^{L}_{i+1/2}=stencil(i-2,i-1,i,i+1,i+2)\\ \cdots\\ f^{L}_{N-3+1/2}=stencil(N-3-2,N-3-1,N-3,N-3+1,N-3+2)\\ f^{L}_{N-2+1/2}=stencil(N-2-2,N-2-1,N-2,N-2+1,N-2+2)\\ f^{L}_{N-1+1/2}=stencil(N-1-2,N-1-1,N-1,N-1+1,N-1+2)\\ \end{array}\end{split}\]

\[\begin{split}\begin{array}{l} f^{L}_{-1/2}\equiv \hat{f}^{L}_{0}=stencil(-3,-2,-1,0,1)\\ f^{L}_{1/2}\equiv \hat{f}^{L}_{1}=stencil(-2,-1,0,1,2)\\ f^{L}_{3/2}\equiv \hat{f}^{L}_{2}=stencil(-1,0,1,2,3)\\ \cdots\\ f^{L}_{i+1/2}\equiv \hat{f}^{L}_{i+1}=stencil(i-2,i-1,i,i+1,i+2)\\ \cdots\\ f^{L}_{N-5/2}\equiv \hat{f}^{L}_{N-2}=stencil(N-5,N-4,N-3,N-2,N-1)\\ f^{L}_{N-3/2}\equiv \hat{f}^{L}_{N-1}=stencil(N-4,N-3,N-2,N-1,N)\\ f^{L}_{N-1/2}\equiv \hat{f}^{L}_{N}=stencil(N-3,N-2,N-1,N,N+1)\\ \end{array}\end{split}\]

Use the periodic boundary conditions

\[\begin{split}\begin{array}{l} f^{L}_{-1/2}\equiv \hat{f}^{L}_{0}=stencil(N-3,N-2,N-1,0,1)\\ f^{L}_{1/2}\equiv \hat{f}^{L}_{1}=stencil(N-2,N-1,0,1,2)\\ f^{L}_{3/2}\equiv \hat{f}^{L}_{2}=stencil(N-1,0,1,2,3)\\ \cdots\\ f^{L}_{i+1/2}\equiv \hat{f}^{L}_{i+1}=stencil(i-2,i-1,i,i+1,i+2)\\ \cdots\\ f^{L}_{N-5/2}\equiv \hat{f}^{L}_{N-2}=stencil(N-5,N-4,N-3,N-2,N-1)\\ f^{L}_{N-3/2}\equiv \hat{f}^{L}_{N-1}=stencil(N-4,N-3,N-2,N-1,0)\\ f^{L}_{N-1/2}\equiv \hat{f}^{L}_{N}=stencil(N-3,N-2,N-1,0,1)\\ \end{array}\end{split}\]

flux at right interface:

\[\begin{split}\begin{array}{l} f^{R}_{-1+1/2}=stencil(-1-1,-1,-1+1,-1+2,-1+3)\\ f^{R}_{0+1/2}=stencil(0-1,0,0+1,0+2,0+3)\\ f^{R}_{1+1/2}=stencil(1-1,1,1+1,1+2,1+3)\\ \cdots\\ f^{R}_{i+1/2}=stencil(i-1,i,i+1,i+2,i+3)\\ \cdots\\ f^{R}_{N-4+1/2}=stencil(N-4-1,N-4,N-4+1,N-4+2,N-4+3)\\ f^{R}_{N-3+1/2}=stencil(N-3-1,N-3,N-3+1,N-3+2,N-3+3)\\ f^{R}_{N-2+1/2}=stencil(N-2-1,N-2,N-2+1,N-2+2,N-2+3)\\ f^{R}_{N-1+1/2}=stencil(N-1-1,N-1,N-1+1,N-1+2,N-1+3)\\ \end{array}\end{split}\]

\[\begin{split}\begin{array}{l} f^{R}_{-1/2}\equiv \hat{f}^{R}_{0}=stencil(-2,-1,0,1,2)\\ f^{R}_{1/2}\equiv \hat{f}^{R}_{1}=stencil(-1,0,1,2,3)\\ f^{R}_{3/2}\equiv \hat{f}^{R}_{2}=stencil(0,1,2,3,4)\\ \cdots\\ f^{R}_{i+1/2}\equiv \hat{f}^{R}_{i+1}=stencil(i-1,i,i+1,i+2,i+3)\\ \cdots\\ f^{R}_{N-7/2}\equiv \hat{f}^{R}_{N-3}=stencil(N-5,N-4,N-3,N-2,N-1)\\ f^{R}_{N-5/2}\equiv \hat{f}^{R}_{N-2}=stencil(N-4,N-3,N-2,N-1,N)\\ f^{R}_{N-3/2}\equiv \hat{f}^{R}_{N-1}=stencil(N-3,N-2,N-1,N,N+1)\\ f^{R}_{N-1/2}\equiv \hat{f}^{R}_{N}=stencil(N-2,N-1,N,N+1,N+2)\\ \end{array}\end{split}\]

Use the periodic boundary conditions

\[\begin{split}\begin{array}{l} f^{R}_{-1/2}\equiv \hat{f}^{R}_{0}=stencil(N-2,N-1,0,1,2)\\ f^{R}_{1/2}\equiv \hat{f}^{R}_{1}=stencil(N-1,0,1,2,3)\\ f^{R}_{3/2}\equiv \hat{f}^{R}_{2}=stencil(0,1,2,3,4)\\ \cdots\\ f^{R}_{i+1/2}\equiv \hat{f}^{R}_{i+1}=stencil(i-1,i,i+1,i+2,i+3)\\ \cdots\\ f^{R}_{N-7/2}\equiv \hat{f}^{R}_{N-3}=stencil(N-5,N-4,N-3,N-2,N-1)\\ f^{R}_{N-5/2}\equiv \hat{f}^{R}_{N-2}=stencil(N-4,N-3,N-2,N-1,0)\\ f^{R}_{N-3/2}\equiv \hat{f}^{R}_{N-1}=stencil(N-3,N-2,N-1,0,1)\\ f^{R}_{N-1/2}\equiv \hat{f}^{R}_{N}=stencil(N-2,N-1,0,1,2)\\ \end{array}\end{split}\]

Riemann Solver: Rusanov Scheme

Riemann solvers are used for accurate and efficient simulations of Euler equations along with higher-order WENO schemes. In this method, first, we reconstruct the left and right side fluxes at the interface similar to the inviscid Burgers equation in non-conservative form. Once we have \(f^{L}_{i+1/2}\) and \(f^{R}_{i+1/2}\) reconstructed, we use Riemann solvers to compute the fluxes at the interface.

We use a simple Rusanov scheme as the Riemann solver. The Rusanov scheme uses maximum local wave propagation speed to compute the flux as follows

\[f_{i+1/2}=\frac{1}{2}(f^{L}_{i+1/2}+f^{R}_{i+1/2})-\frac{1}{2}c_{i+1/2}(u^{R}_{i+1/2}-u^{L}_{i+1/2})\]

where \(f^{L}\) is the flux component using the right reconstructed state \(f^{L}_{i+1/2}=f(u^{L}_{i+1/2})\) and \(f^{R}\) is the flux component using the right reconstructed state \(f^{R}_{i+1/2}=f(u^{R}_{i+1/2})\). Here, \(c_{i+1/2}\) is the local wave propagation speed which is obtained by taking the maximum absolute value of the eigenvalues corresponding to the Jacobian, \(\cfrac{\partial f}{\partial u}=u\), between cells \(i\) and \(i+1\) can be obtained as

\[c_{i+1/2}=\text{max}(|u_{i}|,|u_{i+1}|)\]

or in a wider stencil as shown in Equation

\[c_{i+1/2}=\left | \cfrac{\partial f}{\partial u} \right |=max(|u_{i-2}|,|u_{i-1}|,|u_{i}|,|u_{i+1}|,|u_{i+2}|)\]

flux:

\[\begin{split}\begin{align} f(u) & = \cfrac{u^2}{2}\\ f^{L}_{i+1/2} & = f(u^{L}_{i+1/2}) = \cfrac{({u^{L}_{i+1/2}})^{2}}{2}\\ f^{R}_{i+1/2} & = f(u^{R}_{i+1/2}) = \cfrac{({u^{R}_{i+1/2}})^{2}}{2}\\ \end{align}\end{split}\]

local wave propagation speed:

\[\begin{split}\begin{align} c_{-1+1/2} & = \text{max}(|u_{-1}|,|u_{-1+1}|)\\ c_{0+1/2} & = \text{max}(|u_{0}|,|u_{0+1}|)\\ \cdots\\ c_{i+1/2} & = \text{max}(|u_{i}|,|u_{i+1}|)\\ \cdots\\ c_{N-2+1/2} & = \text{max}(|u_{N-2}|,|u_{N-2+1}|)\\ c_{N-1+1/2} & = \text{max}(|u_{N-1}|,|u_{N-1+1}|)\\ \end{align}\end{split}\]

\[\begin{split}\begin{array}{l} c_{-1/2} \equiv \hat{c}(0) = \text{max}(|u_{-1}|,|u_{0}|)\\ c_{+1/2} \equiv \hat{c}(1) = \text{max}(|u_{0}|,|u_{1}|)\\ \cdots\\ c_{i+1/2} \equiv \hat{c}(i+1) = \text{max}(|u_{i}|,|u_{i+1}|)\\ \cdots\\ c_{N-3/2} \equiv \hat{c}(N-1) = \text{max}(|u_{N-2}|,|u_{N-1}|)\\ c_{N-1/2} \equiv \hat{c}(N) = \text{max}(|u_{N-1}|,|u_{N}|)\\ \end{array}\end{split}\]

\[\begin{split}\begin{array}{l} c_{-1/2} \equiv \hat{c}(0) = \text{max}(|u_{N-1}|,|u_{0}|)\\ c_{+1/2} \equiv \hat{c}(1) = \text{max}(|u_{0}|,|u_{1}|)\\ \cdots\\ c_{i+1/2} \equiv \hat{c}(i+1) = \text{max}(|u_{i}|,|u_{i+1}|)\\ \cdots\\ c_{N-3/2} \equiv \hat{c}(N-1) = \text{max}(|u_{N-2}|,|u_{N-1}|)\\ c_{N-1/2} \equiv \hat{c}(N) = \text{max}(|u_{N-1}|,|u_{0}|)\\ \end{array}\end{split}\]